이번 포스팅에서는 대칭키의 키 배분 문제점을 해결한 공개키 암호화 알고리즘을 소개하려고한다.
비대칭 암호(Asymmetric Cryptography)라고도 불리는데,
두 개의 공개키(Public Key), 비밀 키(Private Key)를 사용한다.
공개 키(Public Key)
공개키 암호학 방식에서 키 생성은 Trap door one way function에 기반을 둔다.
한 방향으로 계산이 쉬우나 다른 방향으로의 계산이 어렵다는 것을 이용한 방식이다.
키를 생성하는데 두 가지의 방법이 존재한다.
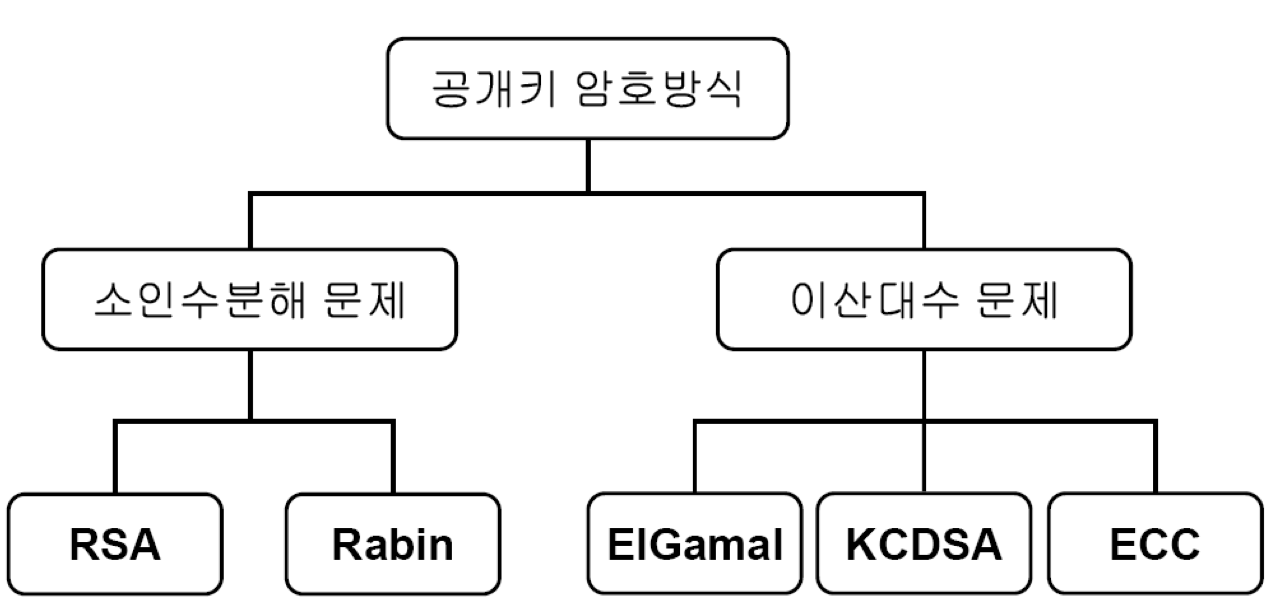
첫 번째로 소인수분해를 이용한 키 생성 방법이 있다.
$$ N\ =\ pq $$
p가 11이고 q가 13일때 N을 구하는 건 간단히 11x13 = 143 간단하게 구할 수 있지만 143을 소수인 p와 q를 구할려면 전자보다 어려워지는 것을 이용한 것이다.
두 번째로 이산대수를 이용한 방법이 존재한다.
$$ y\ =\ g^{x}\ mod\ p $$
g, p, y가 주어져도 해당 x값을 구하는건 어려운 점을 이용한 방법이다.
메시지 암호화
공개키 암호화를 이용해 메시지를 암호화하고 복호화 할 때 대칭키와 달리 키마다 사용용도가 다르다.공개키(Public Key)는 암호화를 하고, 개인키(Private Key)로 복호화를 한다.

위 그림은 Bob이 Alice에게 공개 키 암호화 방식을 이용해 메시지를 보내는 과정을 설명한 그림이다.
- Bob은 “Hello Alice!”라는 메시지를 Alice만 보기를 원한다.
- Alice의 공개 키(Public Key)를 이용해 암호화를 한다.
- Alice는 Bob에게 받은 메시지를 자신의 개인 키로 복호화 한 후 Bob이 보낸 메시지를 확인한다.
RSA
1977년 최초로 공개 키 암호화 방식인 RSA(Rivest-Shamir-Adleman)이 공개되었다.
RSA는 소개된지 40년이 넘은 지금도 널리 사용되고 있다. RSA는 단순히 암호화 뿐만 아니라 디지털 서명에도 사용된다.
- 암호화 - 공개 키(Public Key), 복호화 - 개인키 (Private Key)
- 전자 서명 - 개인 키(Private Key), 서명 검증 - 공개 키(Public Key)
참고로 Bitcoin같은 경우는 RSA와 비슷한 공개 키 암호화 방식인 ECC를 사용한다.
RSA의 암호화체계의 안정성은 큰 숫자를 소인수 분해하는 것이 어렵다는 것에 기반을 두고 있다.
RSA 역시 공개 키 암호화를 소개한 Trap door one way function을 사용해 키 생성을 한다.
RSA 공개 키, 개인 키 구하기
1. 서로 다른 큰 소수 p, q를 선택한다.
2. n을 구한다.
$$ n\ =\ p\ *\ q $$
3. φ(n) => 오일러 Totient 함수, n보다 작은 자연수 중에서 n과 서로 소인 자연수의 개수를 구한다.
φ(n) = (p-1)(q-1)
4. φ(n)보다 작고 φ(n)과 서로소인 임의의 자연수 e를 선택한다.
gcd(e, φ(n)) = 1 (1 < e < φ(n) 만족하는 e를 선택)
5. 확장 유클리드 호제법을 이용해서 e mod φ(n) = 1인 d를 구한다.
RSA는 공개 키를 먼저 구한 다음에 개인 키를 구한다.
(ECC의 경우 RSA와 반대로 개인 키를 먼저 구한 후 공개 키를 구한다.)
- 공개 키(Public Key) : (N, e)
- 개인 키(Private Key) : d
공개 키를 구할 땐 (p-1)(q-1)에 서로소인 e를 찾는다.
RSA 공개 키, 개인 키 구하기
예를들어 p가 11이고 q가 3이라고 하자.
1. N = p * q를 구한다. => n = 33
2. φ(n)=(p-1)(q-1)를 계산한다. => (11-1)(3-1) = 20
3. φ(n)보다 작고 φ(n)과 서로소인 임의의 자연수 e를 선택한다. => e = 3 선택
이 때 20와 서로소 이면서 소수인 3을 선택한다. e = 3
ed = 1 mod (p-1)(q-1)에서 ed = 1 mod 20이 된다.
따라서 d = 7이다. (e가 3이므로)
- 공개 키 (N, e) : (33, 3)
- 개인 키 d : 7
RSA 사용
- 메시지 M의 암호화
$$ C=M^{e}\ mod\ {N} $$
- 암호문 C의 복호화
$$ M=C^{d}\ mod\ N $$
위의 식을 이용하면 간단하게 RSA를 사용해 볼 수 있다.
메시지 M = 8일 때,
위 예제에 나왔던 공개 키와 개인 키를 이용해서 암호화를 진행해 보겠다.
$$ C=M^{e}\ mod\ N\ =\ 8^{3}\ mod\ 33\ =\ 17\ mod\ 33$$
따라서 암호문 C = 17이다.
복호화도 마찬가지로 위에 식을 이용하면된다.
$$ M=C^{d}\ mod\ N\ =\ 17^{7}\ mod\ 33\ =\ 8\ mod\ 33$$
이 결과로 처음 메시지였던 M = 8을 얻을 수 있다.
Diffie-Hellman
Diffie-Hellman은 RSA처럼 암호화나 서명을 위한 것이 아닌 키 교환 알고리즘이다.
1976년에 스탠퍼드 대학교 연구자 Diffie와 Hellman이 공개한 논문인데 그들은 공개 키 분배 방안이라는 이름의 프로토콜을 소개했다.
DH 프로토콜이라고 부른다.
Diffie-Hellman 프로토콜은 통신 당사자들이 DH 프로토콜을 이용해 한 가지의 비밀을 공유하고 나면, 보안 채널(Secure Channel)을 만들 수 있다. 즉, 그 비밀을 하나 이상의 대칭 키들로 변환을 하고 이후의 통신 내용을 암호화, 인증해서 안전하게 통신을 진행할 수 있는 것이다.
Diffie-Hellman의 키 교환 암호화 알고리즘의 안전성은 이산대수 문제 (discrete log problem)에 달려있다.
$$ g^{k}\ mod\ p\ =\ x $$
x, g, p가 주어졌을 때 k를 구하기 어려운 것을 이용함.
Diffie-Hellman 방식
철수와 영희가 공개된 통신망에서 Diffie-Hellman 키 교환을 하기 위해 다음과 같은 절차를 거친다.
p는 소수, g는 generator이다.
1.철수가 소수 p, 그리고 1 ~ p-1까지의 정수 g를 선택하여 사전에 영희와 공유한다.
(g와 p는 공개한다.)
2.철수는 비밀 값 a, 영희는 비밀 값 b를 선택한다. 이 비밀 값은 외부에 공개하지 않는다.
3.철수는 영희에게 아래 식을 보낸다.
$$ g^{a}\ mod\ p $$
4.영희도 철수에게 아래 식을 보낸다.
$$ g^{b}\ mod\ p $$
5. 둘 다 비밀 값을 대칭 키로 사용한다.
$$ g^{ab}\ mod\ p $$
Diffie-Hellman의 문제점
Man-in-the-middle(MiM)공격
Diffie-Hellan은 MiM의 공격 위험에 노출되어있다.

-
Trudy는 Alice와 비밀 키를 공유
$$ g^{at}\ mod\ p $$ -
Trudy는 Bob과 비밀키를 공유
$$ g^{bt}\ mod\ p $$ -
이때 Alice와 Bob은 Trudy의 존재를 모른다.
해결방안
-
교환하는 값을 대칭키로 암호화하여 보낸다.
$$ g^{a}\ mod\ p,\ g^{b}\ mod\ p $$ -
교환하는 값을 공개키로 암호화해서 보낸다.
-
교환하는 값을 개인키로 서명
-
공인인증서처럼 믿을 수 있는 기관을 중간에 둔다. -> PKI
공개키 구조(PKI)
공개 키(Public Key)는 모든 사람이 알 수 있는 키이다.
만약에 Alice가 Bob에게 메시지를 보내기 위해서는 Bob의 공개 키를 사용해야한다.
이때 Alice는 Bob의 공개키가 맞는지에 대한 문제점과 중간에 공격자가 공개키를 가로채 다른 공개키를 전달할 수 있는 문제가 생긴다. (Man in the middle attack)
따라서 Bob의 이름과 Bob의 공개 키(Public Key)를 포함하는 인증서(Certificate)를 사용한다.
인증서를 제공하는 발행자(Certificate Authority)가 이 것을 보증하기 위해서 인증서에 서명을 한다.
Public blockChain에서는 공개 키 구조(PKI)를 사용하면 안된다. Private BlockChain에 사용해야 한다.
그렇다면 인증서를 발급하고 인증서에 대한 보증을 하는 사람 혹은 기관이 필요하다.
공개키 구조(PKI)에서는 인증 기관(Certificate Authority)인 신뢰할 수 있는 제 3자가 인증서를 발행하고 서명한다.
공개 키 암호화의 활용
1. 메시지 암호화
안전하지 않은 경로로 통신을 할 때 데이터의 기밀성을 보장할 수 있다.

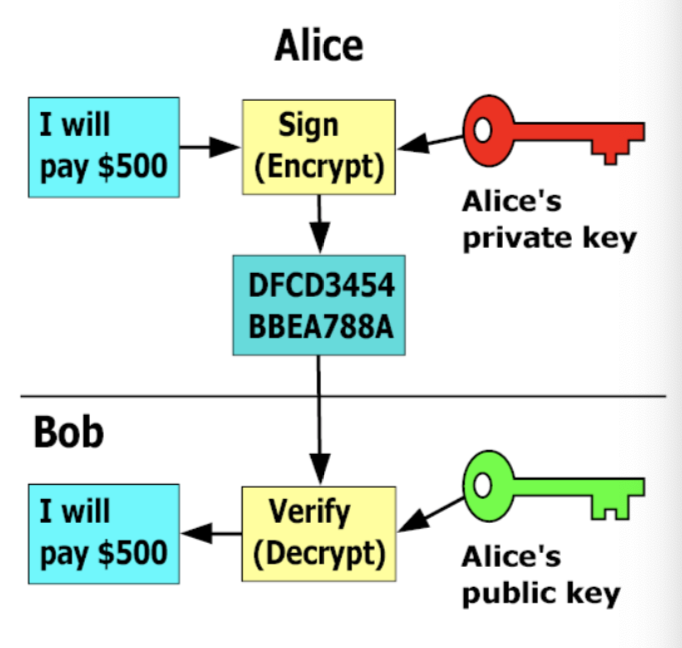
2. 전자 서명
전자서명(Digital Signature)을 통해 메시지의 무결성을 인증해준다. 그리고 부인(repudiation)을 방지한다.
ex) 인증서가 있을 때 서명을 할 때 고유한 개인키로 서명을 하는데 만약에 Alice가 이 메시지는 자신것이 아니라고 주장할 수 없다.
이미 자신의 개인키로 서명을 하였기 때문이다.
대칭 키 vs 공개 키
- 대칭 키의 장점
- 속도
- 공개키 구조(PKI)가 필요가 없다.
- 공개 키의 장점
- 서명
- 키 관리가 쉽다.
Bitcoin과 Ethereum에서 쓰이는 전자서명 알고리즘인 ECC는 다음 포스팅에서 소개하겠습니다.
참고자료
- 처음 배우는 암호학 알고리즘 (한빛 미디어)
- 디피-헬먼 키 교환 : https://ko.wikipedia.org/wiki/%EB%94%94%ED%94%BC-%ED%97%AC%EB%A8%BC_%ED%82%A4_%EA%B5%90%ED%99%98
- RSA 암호 : https://ko.wikipedia.org/wiki/RSA_%EC%95%94%ED%98%B8
'블록체인 > 암호학' 카테고리의 다른 글
| 모듈러 연산 (Modular arithmetic) (5) | 2019.04.13 |
|---|---|
| 기초 암호학(4) - ECC(타원곡선 암호화 알고리즘) (3) | 2019.04.13 |
| 기초 암호학(2) - AES (0) | 2019.03.01 |
| 기초 암호학(1) - DES (4) | 2019.02.24 |
| Hash 함수를 알아보자 (3) | 2018.11.27 |



댓글