블록체인을 공부하다 보면 자주 접하는 암호화 알고리즘입니다.
암호화 알고리즘RSA 암호방식에 대한 대안으로 1985년에 제안되었습니다.
암호키 길이가 길어지면 보안 강도는 높아지지만 속도가 느려집니다.
하지만, ECC(Elliptic Curve Cryptography)를 사용하면 짧은 키로도 동일한 암호 성능을 가지는데, 이는 컴퓨터 성능이 낮아도 암호 성능을 유지할 수 있게되었습니다.
따라서, 이러한 이유로 RSA를 대체할 차세대 공개키 암호기술로 부상하고 있다.
타원 곡선 암호화(Elliptic Curve) 알고리즘으로 불리며, 이전 포스팅에서 소개했던 공개키 암호화 방식입니다.
타원 곡선의 정의
아래 방정식을 만족하는 x, y의 집합을 곡선 그래프로 나타낸 것을 뜻합니다.
$$ y^{2}\ =\ x^{3}+ax+b $$

타원곡선 그래프를 보다보면 흥미로운 특징을 가지고 있습니다.
x축을 중심으로 대칭되며, 비 수직선에 대해 최대 3개 지점에서 곡선과 교차한다는 점이다.

타원 곡선 상에서의 연산
타원 곡선을 이용한 암호화 알고리즘을 알기 위해서는 타원 곡선 상의 덧셈 연산을 이해하여야 합니다.
간단한 예시로 타원곡선상의 P와 Q의 덧셈연산을 설명하자면, P와 Q를 지나는 직선이 타원과 만나는 교점(R)을 x축으로 대칭시킨 점을 P + Q = R로 정의합니다.
아래 그림의 그래프(b)는 같은 값을 가지고 있는 P를 구하는 타원 곡선입니다.
덧셈 연산과 같이 P의 접접을 타원 곡선으로 이은 교점(R)을 x축으로 대칭시킨 점을 2P = R로 정의합니다.


GF 상에서의 타원 곡선(Elliptic Curves Over GF(p))
GF는 유한체(Finite Field)를 의미하는데 유한개의 원소를 가지는 체를 뜻합니다.
x, y과 좌표계에서 무한하지 않고 유한하게 한정된 곳에 존재하는데, GF를 만들기 위해 모듈러(Modular)를 사용합니다.
$$ E\ :\ y^{2}\ =\ x^{3}\ +\ x\ over\ Z_{23} $$

위의 그림은 p가 23일때 GF상에 존재하는 모든 좌표를 나타냈습니다.
만약 x = 11일때,
$$ y^2\ mod\ 23\ =\ (1331\ +\ 11)\ mod\ 23 =\ 1342\ mod\ 23\ =\ 8 $$
이때 만족하는 y의 값을 구하려면
$$ y^2\ mod\ 23\ =\ 8 $$
위의 식을 구해야 하는데, y의 값이 될 수 있는 건 10과 13입니다.
이때 GF의 필드의 p가 커진다면 y를 찾기 힘들어지는데, 이러한 점을 이용하여 암호화를 수행할 수 있습니다.
타원곡선 암호화 알고리즘 키생성
G : 생성자, 타원곡선 상의 임의의 점
x : 개인키, P보다 작은 소수(Prime)로, 난수 생성기로 생성
Q : 공개키, 개인키로부터 연산
점 P=(x, y)가 타원곡선 상에 위치해 있을 때 두 점 P, Q와 임의의 정수 x에 대해 다음과 같은 방정식을 정의할 수 있습니다.
$$ Q\ =\ xG $$
이때 x의 값을 구하는 것이 타원곡선 이산대수 문제인데, 공개키 Q는 Q = xG = G + G + ... + G 으로 G를 x번 덧셈을 한 값입니다.
Q = xG 수식에서 x와 G를 이용하여 Q를 구하기 쉽지만, 알려진 G값과 Q값을 통해 x값을 구하기 어려운 점을 이용합니다.
이러한 것을 ECDLP(Elliptic Curve Discrete Logarithm Problem)라고 부르며, 이러한 속성으로 인해 공개 키 암호기술로 사용됩니다.
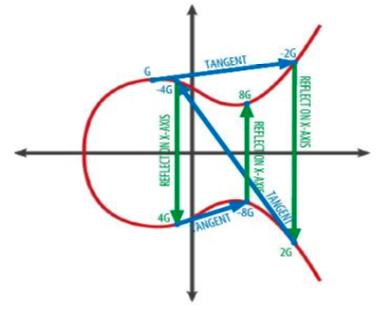
위의 그림은 xG의 연산 과정을 기하학적으로 도식화한 그래프입니다.
앞에서 소개한 타원곡선 암호화 알고리즘(ECC)의 덧셈연산에서 P를 doubling한 2P를 보면 2G = G + G는 점 G에서의 접선이 타원곡선과 만나는 점을 x축으로 대칭시킨 지점입니다.
4G = 2G + 2G는 2G에 해당하는 점에서 마찬가지로 접선을 그어 타원 곡선과 만나는 점의 x축 대칭 점입니다.
G의 상수 배 연산은 이를 반복적으로 수행 할 수 있습니다.
타원곡선은 공개키 암호 체계를 수학적으로 수행하는 방법 중 한가지인데, 타원곡선을 이용해서 RSA, ElGamal, Diffie-Hellman을 구현할 수 있습니다.
예제를 통해 타원곡선 알고리즘을 통해 키를 생성하는 것을 알아보겠습니다.
주어진 식은 아래와 같습니다.
$$ E:\ y^{2}\ =\ x^{3}\ +\ x\ +\ 6\ over\ Z_{11} $$
$$ G(\alpha)\ =\ (2,7) $$
$$ 2\alpha\ =\ (x_{2},y_{2}) $$
2α를 구한다면,

$$ 2\alpha\ =\ (5, 2) $$
이 방법을 이용해 α, 2α, ... , kα를 구할 수 있습니다.
비밀키(x) * α = 공개키(Q)
다른 암호화 알고리즘과 암호화 강도 비교
ECC를 사용하면 더 적은 bit수로 동일한 암호 성능을 낼 수 있습니다.
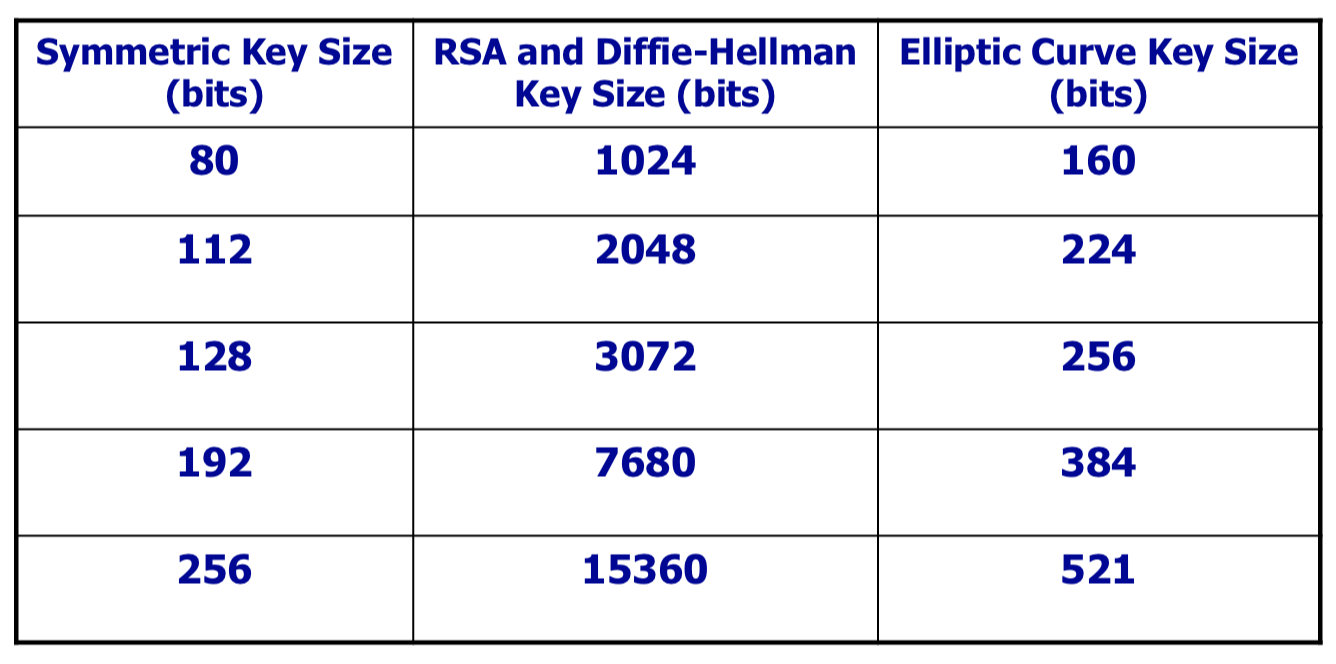
ECC의 160bit키는 RSA나 Diffie-Hellman에서 사용되는 키인 1024bit와 동일한 암호 성능을 나타냅니다.
참고자료
Elliptic-curve cryptography : https://en.wikipedia.org/wiki/Elliptic-curve_cryptography
비 대칭키 암호 : http://slidesplayer.org/slide/11329530
'블록체인 > 암호학' 카테고리의 다른 글
| 모듈러 연산 (Modular arithmetic) (5) | 2019.04.13 |
|---|---|
| 기초 암호학(3) - 공개키 암호 (RSA, Diffie-Helmman) (3) | 2019.03.27 |
| 기초 암호학(2) - AES (0) | 2019.03.01 |
| 기초 암호학(1) - DES (4) | 2019.02.24 |
| Hash 함수를 알아보자 (3) | 2018.11.27 |



댓글